来自于LeetCode liweiwei1419
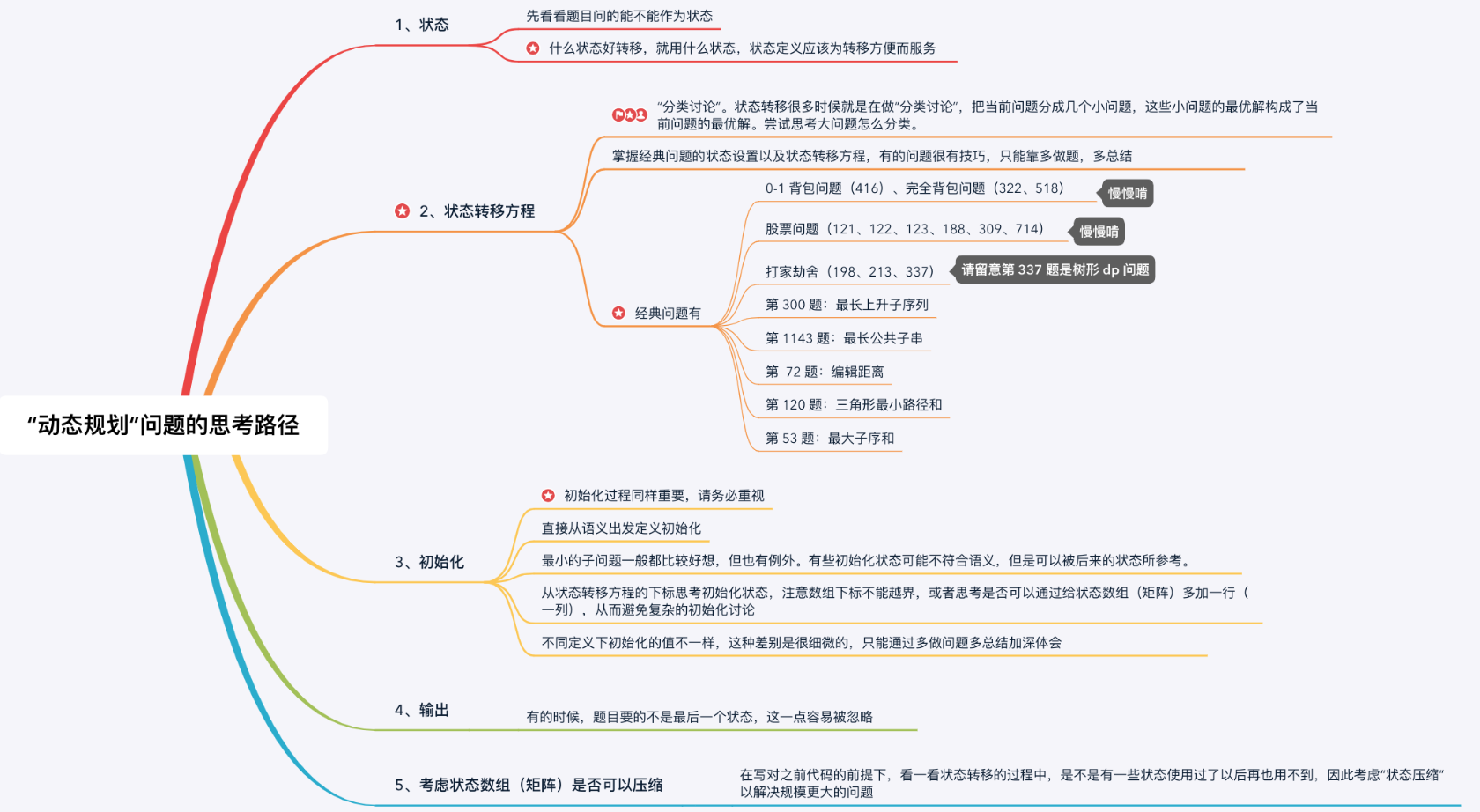
股票问题通用解法自我总结
以188号问题为例:
题目:
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
注意: 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
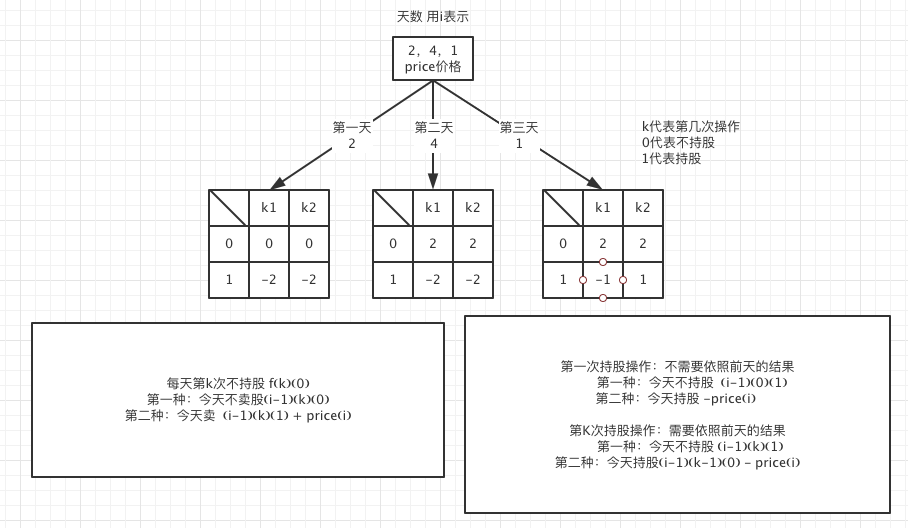
输入: [2,4,1], k = 2
输出: 2
解释: 在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
示例 2:
输入: [3,2,6,5,0,3], k = 2
输出: 7
解释: 在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。 随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
自我总结
动态规划的问题首先要确定状态和转移方程
1.状态
阶段:即时股票每天的价格用i表示
状态1:即处在第几个交易用k表示
状态2:即现在是持股还是不持股。设置持股的状态值为 1,不持股的时候,状态值为 0。
为此设计状态如下:
dp[i][k][0] :表示到第 i 天为止,已经交易了 k 次,并且当前持股状态的最大收益。
dp[i][k][1] :表示到第 i 天为止,已经交易了 K 次,并且当前不持股状态的最大收益。
2.转移方程
下面考虑 dp[i][k][0] 和 dp[i][k][1] 可以怎样转移过来。
动态规划用于解决多阶段的决策问题,这里的阶段就是每一天,因此,状态都是从前一天的某一个之前的状态转移过来。
dp[i][k][0]:表示这一天发生了第 k 次交易(从 0 开始),并且不持股。
交易行为:发生交易的标志是在某一天有了一次购买行股票的为,视为发生一次交易。发生一次抛售股票的行为,认为和上一次购买股票在一次交易行为内。
分类讨论的依据是:昨天是否持股。
- 昨天不持股,今天还不持股,说明没有发生新的交易;
- 昨天持股,今天不持股,说明这次交易结束了。这两种情况都在一次交易里。
二者取最大值,即:
dp[i][k][0] = max(dp[i - 1][k][0], dp[i - 1][k][1] + prices[i])
注意:中间的那个表示交易次数的状态都是 k。
dp[i][k][1]:表示这一天发生了第 k 次交易(从 0 开始),并且持股。
分类讨论的依据依然是:昨天是否持股。
- 昨天持股,今天还持股,说明没有发生新的交易,这两天在同一个交易区间里;
- 昨天不持股,今天持股,说明开启了一次新的交易。
二者取最大值,即:
dp[i][k][1] = max(dp[i - 1][k][1], dp[i - 1][k - 1][0] - prices[i])
代码
public int maxProfit(int k, int[] prices) {
int len = prices.length;
if(len < 2 || k == 0)
return 0;
if (k >= len / 2)
return greedy(prices, len);
int[][][] dp = new int[len][k][2];
for(int i = 0;i < len; i++){
for(int j = 0;j < k;j++){
if(i == 0){
dp[i][j][0] = 0;
dp[i][j][1] = -prices[0];
}else{
//第一次操作
if(j == 0){
dp[i][j][1] = Math.max(dp[i - 1][0][1], -prices[i]);
}else{
dp[i][j][1] = Math.max(dp[i - 1][j][1],dp[i - 1][j - 1][0] - prices[i]);
}
dp[i][j][0] = Math.max(dp[i - 1][j][0],dp[i-1][j][1] + prices[i]);
}
}
}
return dp[len - 1][k - 1][0];
}
private int greedy(int[] prices, int len) {
int res = 0;
for (int i = 1; i < len; i++) {
if (prices[i - 1] < prices[i]) {
res += prices[i] - prices[i - 1];
}
}
return res;
}
